What is the Present Value of Annuity? An annuity's present value is calculated by discounting each future payment to today's value. It is beneficial for calculating the worth of a series of fixed charges paid over a given period. Value these future payments in today's money by figuring out their present value. The time value of money is the idea that money in hand now is worth more than the same amount in the future because of the opportunity cost of waiting to spend or invest it. Getting paid directly is often favored over getting paid later for the same amount. The cash flow amount, the frequency of payments, the duration of the annuity, and the proper discount rate are all important considerations when determining the present value of a grant.
How Money Changes Over Time
It would be best if you had a firm grasp of the time value of money to calculate the present value of an annuity. Simply put, the time value of money acknowledges that a dollar today is worth more than a dollar in the future. The availability of expansion or investment options inspires this guiding idea. Inflation, interest rates, and the opportunity cost of investing money elsewhere all play a role in determining the worth of money over time. It provides a framework for assessing the value of future cash flows in light of their present value, which is essential for making sound financial decisions.
Annuity: Definition And Types
A financial annuity is a contract for a series of fixed payments over a period. These inflows and outflows can happen simultaneously every month or year. Retirement preparation, insurance, and structured settlement payments are typical annuity applications. Ordinary annuities and annuities due are the two most common types of annuities. Payments for ordinary annuities are made at the end of each period, while payments for annuities due are made at the start of each period. When figuring out the present value of an annuity, it helps to know the difference between these two categories.
Annuity Present Value Formula
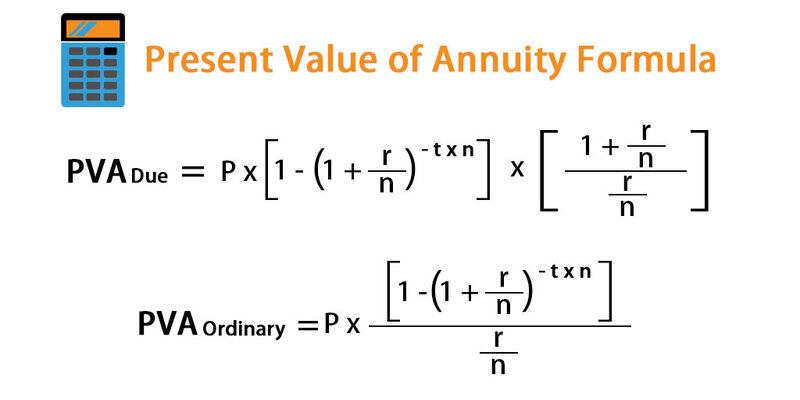
Future cash flows are discounted back to their present value using a mathematical formula to determine the current value of an annuity. The formula considers cash flow amount, payment frequency, annuity term, and discount rate.
Here is the formula for calculating the present value of an annuity:
To calculate PVA, multiply C by [(1 - (1 + r)-n) / r].
Where:
Value of Annuity at Present Time
C = Net Cash Inflow
r = Periodic Interest Rate (Discount Rate).
n = Total period
We will examine each part of the formula in detail, discussing its function and impact on the final present value. We will also explore alternatives to the basic recipe for exceptional cases like perpetuities and increasing annuities.
Applications And The Value Of Annuities At Present
Calculating the present value of an annuity is helpful in many areas of finance, including personal budgeting, business management, and investment strategy. In this section, we'll examine various essential use cases for the concept:
The present value of an annuity is a valuable tool for retirement planners in estimating how much money would be needed in retirement. Individuals can make educated decisions regarding their retirement savings and investing strategies by calculating the present value of their future pension payments, Social Security benefits, or other sources of retirement income. Comparison of Loan Terms, Interest Rates, and Payment Schedules Present value of the annuity is a valuable tool for borrowers to use when evaluating loan options.
Factors Influencing Annuity Present Value

The present value of an annuity depends on several different variables. To completely appreciate the concept, it is crucial to consider these variables. Important considerations include:
The opportunity cost of money invested elsewhere, or the rate of return sought, is known as the discount rate. When the discount rate is increased, the present value of an annuity decreases because the future cash flows are discounted at a higher rate. However, the current value goes up if the discount rate goes down. To determine the present value of an annuity series, it is necessary to know the amount of each cash flow. A more excellent current value is achieved by having more significant cash flows, while a lower present value is achieved by having smaller cash flows.
Conclusion
The present value of an annuity allows consumers and businesses to determine the current value of future income payments. To make sound financial decisions, it is crucial to have a firm grasp of the concept of the time value of money, the formula for calculating it, and the many elements that affect the present value. The current value of an annuity provides a valuable framework for assessing the monetary value of recurring payment flows over time, which can be applied in various contexts, such as retirement planning, loan evaluation, investment analysis, and business valuation. The present value of an annuity can be used to negotiate financial difficulties and optimize long-term economic outcomes successfully.




